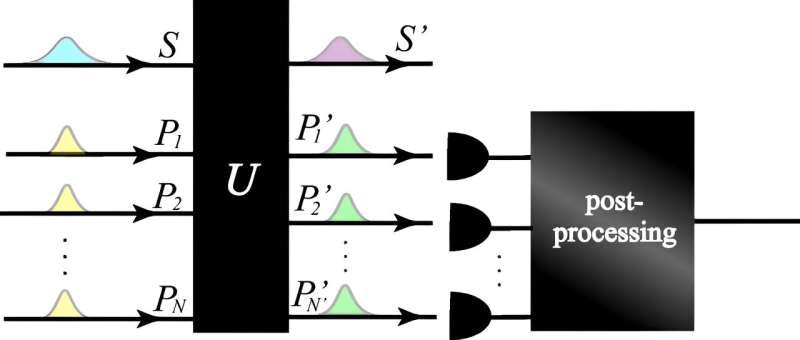
Модель измерения с пассивными оптическими процессами и измерениями подсчета фотонов. кредит: Письма о физическом осмотре (2023). doi: 10.1103/PhysRevLett.131.210201
изучать опубликовано В журнале Письма о физическом осмотре исследователями из Японии решает давнюю проблему квантовой физики, переопределяя принцип неопределенности.
Принцип неопределенности Вернера Гейзенберга — фундаментальная и удивительная особенность квантовой механики, и за это он может поблагодарить свою сенную лихорадку. Летом 1925 года молодой немецкий физик тосковал в Берлине, отдыхая на отдаленном скалистом острове Гельголанд в Северном море у северного побережья Германии. Его чувствительность улучшилась, и он смог продолжить свою работу, пытаясь понять сложности модели атома Бора и разработать таблицы внутренних свойств атома, таких как энергия, положение и импульс.
Когда он вернулся в Геттинген, его советник Макс Борн понял, что каждую из этих таблиц можно преобразовать в матрицу — по сути, в двумерную таблицу значений. Вместе с 22-летним Паскуале Йордансом они усовершенствовали свои работы по матричной механике — первой успешной теории квантовой механики — физических законов, описывающих небольшие объекты, такие как атомы и электроны.
Хотя через несколько лет матричная механика была заменена волновой функцией Шредингера и ее уравнением, она дала Гейзенбергу понимание формулировки принципа неопределенности: существует предел того, насколько точно могут быть определены положение и импульс квантовой системы, обычно частицы. . измерение.
Термин, обозначающий произведение измерений неопределенности двух величин, равен h/4π, где h — постоянная Планка, которая очень мала, но, тем не менее, не равна нулю. Короче говоря, невозможно измерить положение и импульс квантового объекта с произвольной точностью — измерение одного с более высокой точностью означает, что другое можно измерить только с меньшей точностью.
С точки зрения физики, скажем, мы хотим измерить положение и импульс электрона. Необходимо каким-то образом пролить свет на систему, чтобы измерить ее свойства. Свет измеряется в виде фотонов, которые имеют ненулевую энергию. Облучение фотона электроном обязательно приводит к выводу электрона из исходного состояния. В квантовой механике само измерение накладывает ограничение на точность измерения.
Аналогичные неопределенности применимы к измерениям времени и энергии, углового положения и углового момента, а также к любым двум переменным, которые не «движутся», когда они представлены в виде персонал В строгой квантовой механике.
Несколько десятилетий спустя принцип неопределенности был уточнен физиками Юджином Вигнером, затем Хосехиро Араки и Муцу М. Янассе в теореме Вигнера-Араки-Янасси (WAY), которая утверждает, что для двух наблюдаемых величин q и p, где p сохраняется (например, импульс системы), даже если p вообще не измеряется, q не может быть измерено. измеряется с произвольной точностью.
«В результате теоремы WAY мы видим, что (в определенном смысле) невозможно измерить положение частицы q; все, что мы можем измерить, — это ее положение относительно устройства q—Q», — сказал математик Джон Байеса из Калифорнийского университета. Калифорнийский университет в Риверсайде имеет написаногде Q – положение измерительного устройства.
Но теорема УЭЯ применима только к таким величинам, как спин частицы, который может принимать только дискретные и конечные величины.
Теперь Юи Курамоти из Университета Кюсю и Хироясу Тадзима из Университета электрических коммуникаций в Японии решили давнюю проблему, показав, что теорема WAY также применима к наблюдаемым величинам, которые являются непрерывными (недискретными) или бесконечными, такими как положение .
«Согласно принципу неопределенности, положение и импульс не могут быть точно измерены одновременно», — сказал Курамочи. «Наши результаты накладывают дополнительное ограничение: даже само положение не может быть точно измерено, пока мы используем обычные измерения, которые удовлетворяют закону сохранения импульса». Их доказательство исследует «бесконечный фактор» — физические величины, которые могут принимать бесконечно большие значения.
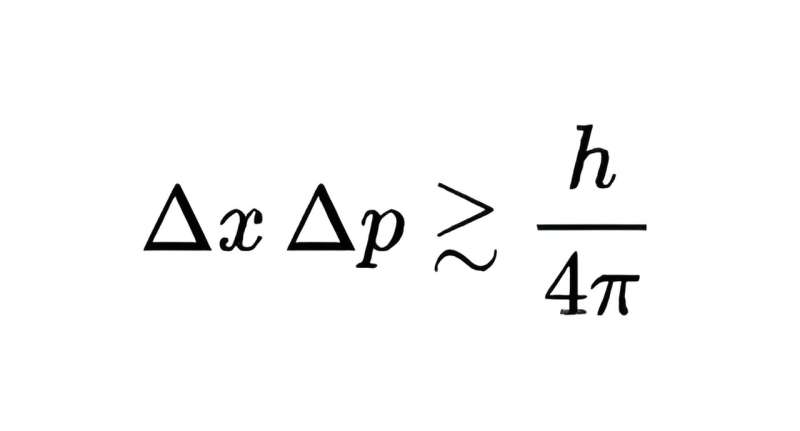
Типичная формулировка принципа неопределенности. Источник изображения: Википедия, https://simple.wikipedia.org/wiki/Uncertainty_principle, лицензия Creative Commons Attribution-ShareAlike: https://creativecommons.org/licenses/by-sa/4.0/
Строго говоря, для получения результата требуется определенное условие, лежащее в основе теоремы WAY, называемое условием Янасэ. Хотя это очень технический вопрос, в основном он утверждает, что неограниченная переменная устройства совместима с сохраненным количеством. Условие Янаса, хотя и математическое, кажется желательным при применении к реальным физическим системам.
«Теория WAY предсказывает, что по закону сохранения физическая величина, которая не перемещается с сохраняющимся зарядом, не может быть измерена без ошибок», — продолжает Курамочи. «Это согласуется с ответом на проблему, которая была открыта в течение 60 лет. Новый результат решает многолетнюю проблему того, как бороться с такими непрерывными и неограниченными наблюдениями, особенно в таких областях, как квантовая оптика, где расширение новая теория, вероятно, найдет применение».
Исходная теорема WAY не позволяет ошибке измерения быть равной нулю, но это качественная теория и не определяет предел измерения или даже то, существует ли нижний предел, превышающий ноль. То же самое относится и к расширению теории ПУТИ Курамочи и Тадзимой.
Авторы пишут в своей статье, что до сих пор остается открытым вопрос, можно ли обобщить исходную теорию WAY для повторных измерений, как они это сделали, на бесконечное количество сохраненных наблюдений.
Предлагая новые направления исследования расширений теории WAY, команда хотела бы обобщить свои результаты на случаи с ограниченной энергией, где их текущие результаты ограничены случаями, независимыми от состояния, и приближенными случаями. Одним из потенциальных применений является установление ограничений на то, насколько транспортные протоколы квантовых сетей могут работать лучше, чем классические ограничения.
Дополнительная информация:
Юи Курамочи и др., Теория Вигнера-Араки-Янасси непрерывных и бесконечных сохранившихся наблюдений, Письма о физическом осмотре (2023). doi: 10.1103/PhysRevLett.131.210201
© 2023 Веб оф Сайенс
цитата: Расширение принципа неопределенности с использованием неограниченного оператора (14 декабря 2023 г.). Получено 14 декабря 2023 г. с https://phys.org/news/2023-12-uncertainty-principle-unbounded.html.
Этот документ защищен авторским правом. Несмотря на любые добросовестные действия в целях частного изучения или исследования, никакая часть не может быть воспроизведена без письменного разрешения. Содержимое предоставлено исключительно в информационных целях.

«Главный евангелист пива. Первопроходец в области кофе на протяжении всей жизни. Сертифицированный защитник Твиттера. Интернетоголик. Практикующий путешественник».






More Stories
Ученые раскрыли секреты потери морских звезд и возобновления роста конечностей
Комплексное мероприятие сообщества людей с деменцией в Ратуте, посвященное Всемирному месяцу борьбы с болезнью Альцгеймера.
Новое исследование массивного надвига предполагает, что следующее большое землетрясение может быть неизбежным